算法学习笔记(28): 网络流

2024-08-20 00:12:11 19

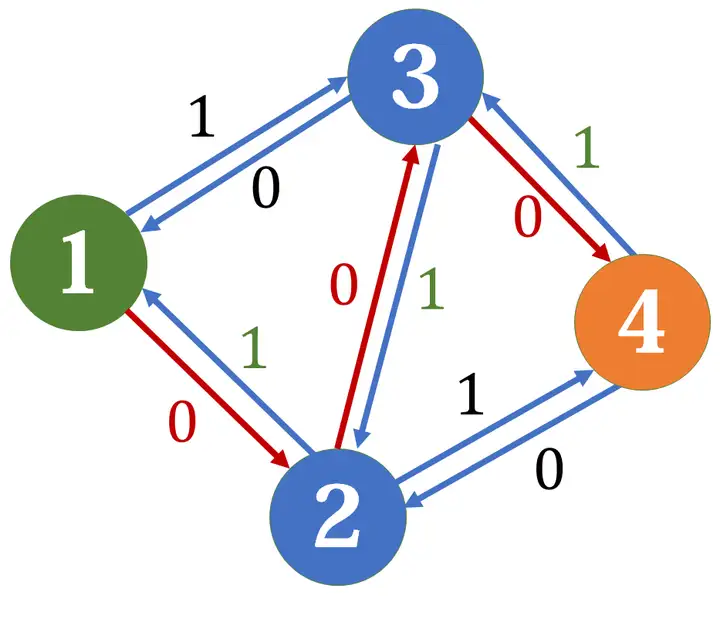
网络流是算法竞赛中的一个重要的模型，它分为两部分：网络和流。

网络，其实就是一张有向图，其上的边权称为容量。额外地，它拥有一个源点和汇点。

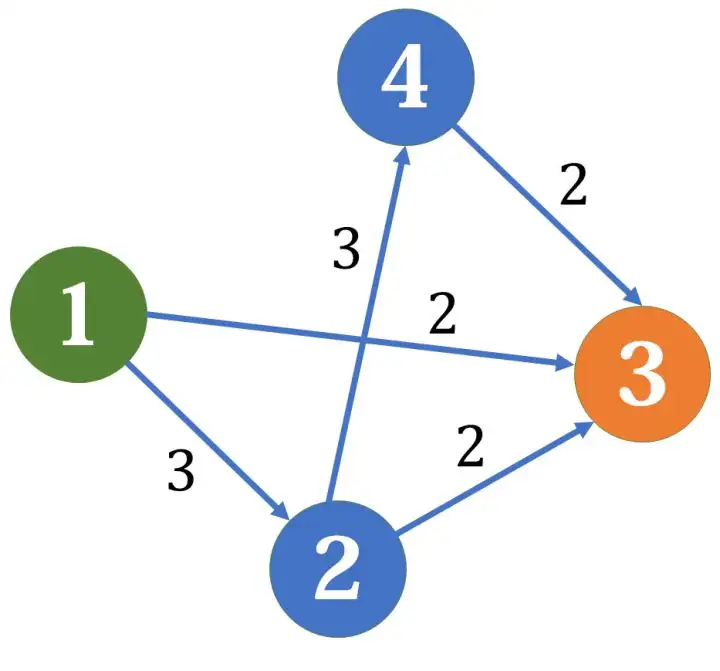
其中1为源点，3为汇点

流，顾名思义，就像水流或电流，也具有它们的性质。如果把网络想象成一个自来水管道网络，那流就是其中流动的水。每条边上的流不能超过它的容量，并且对于除了源点和汇点外的所有点（即中继点），流入的流量都等于流出的流量。

网络流中最常见的问题就是网络最大流。假定从源点流出的流量足够多，求能够流入汇点的最大流量。例如对上面那张网络而言，最大流是5，其中1->3提供2流量，1->2->3提供2流量（这有点像木桶原理，某条路径的容量是由最窄的一根水管决定的），1->2->4->3提供1流量（注意这里不是2，因为上条路径已经占用了1->2的2单位容量，只剩1单位容量可用）。

解决这个问题最常用的是Ford-Fulkerson算法及其优化。

Ford-Fulkerson算法

FF算法的核心在于找增广路。何谓增广路？例如上图中我首先选择1->2->3，这是一条增广路，提供2流量；然后我们相应地扣除选择路径上各边的容量，1->2的容量变成1，2->3的容量变成0，这时的容量称为残余容量。然后我们再找到1->2->4->3这条路径，按残余容量计算流量，它提供1流量（选择这两条路的顺序可以颠倒）。1->2->4->3也是一条增广路。

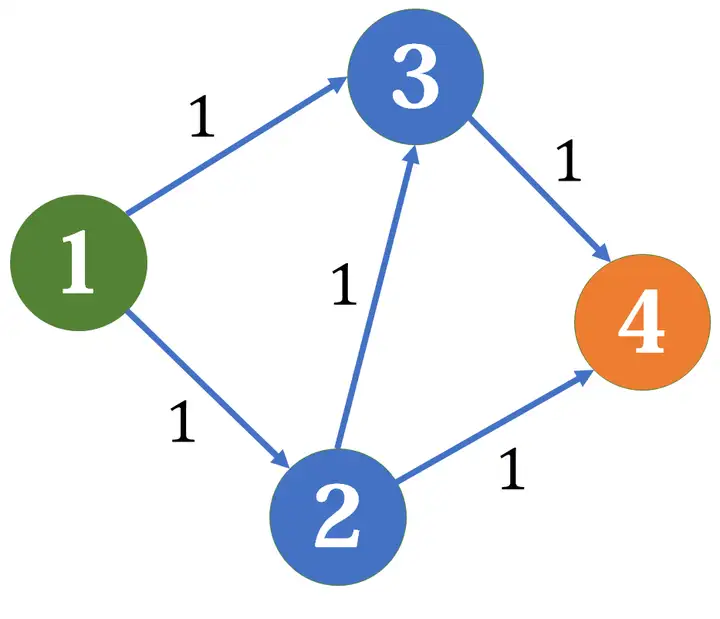
增广路，是从源点到汇点的路径，其上所有边的残余容量均大于0。FF算法就是不断寻找增广路，直到找不到为止。这个算法一定是正确的吗？好像不一定吧，比如这张图……

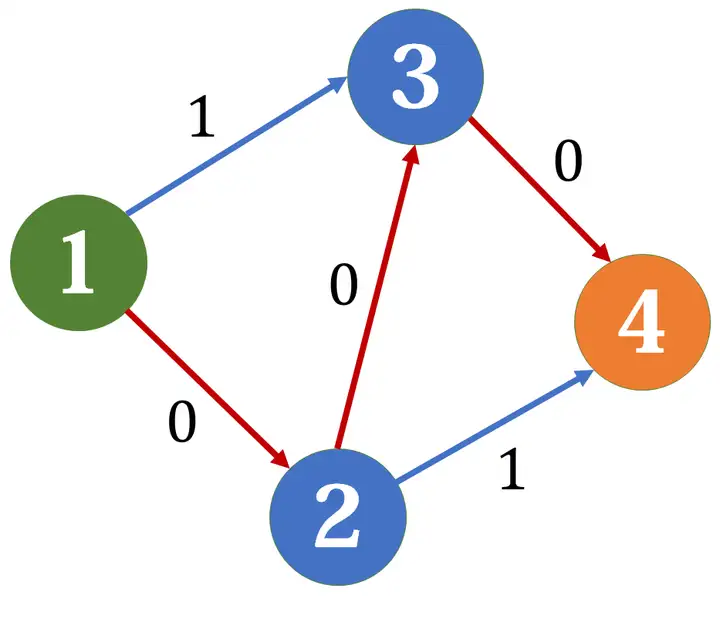
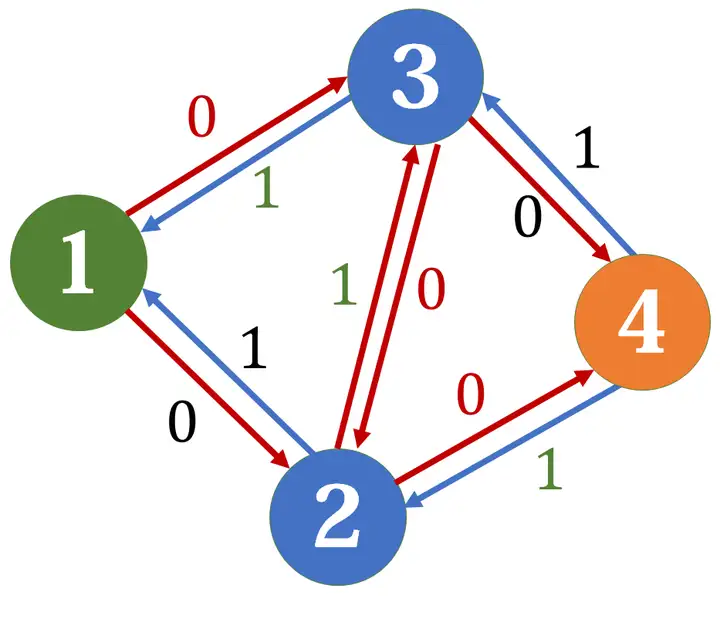
如果我们首先找到了1->2->3->4这条边，那么残余网络会变成这样：

现在已经找不到任何增广路了，最终求得最大流是1。但是，很明显，如果我们分别走1->3->4和1->2->4，是可以得到2的最大流的。

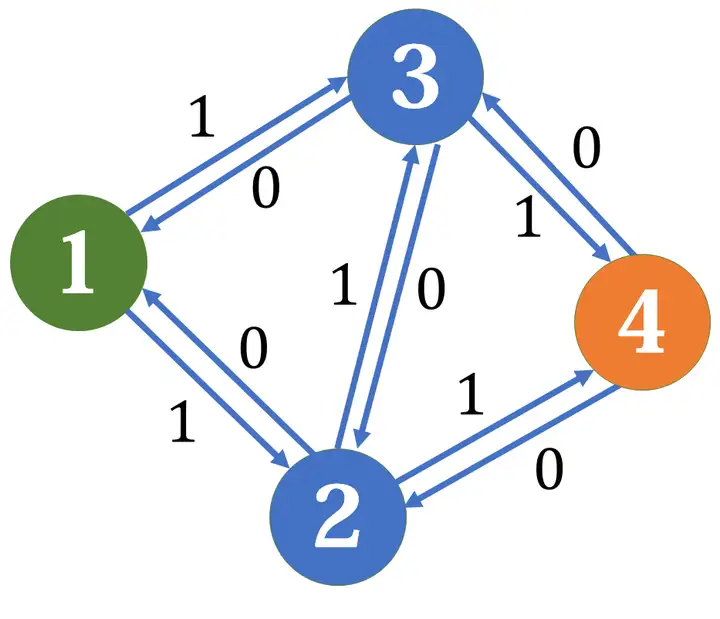
为了解决这个问题，我们引入反向边。在建边的同时，在反方向建一条边权为0的边：

我们仍然选择1->2->3->4，但在扣除正向边的容量时，反向边要加上等量的容量。

这时我们可以另外找到一条增广路：1->3->2->4。

注意看，现在我们同时选择了2->3和3->2两条边，我们可以认为，这两条边上的水流抵消了。所以实际上选择的路径就是1->3->4和1->2->4。

其实可以把反向边理解成一种撤销，走反向边就意味着撤回上次流经正向边的若干流量，这也合理解释了为什么扣除正向边容量时要给反向边加上相应的容量：反向边的容量意味着可以撤回的量。

加入了反向边这种反悔机制后，我们就可以保证，当找不到增广路的时候，流到汇点的流量就是最大流。

用dfs实现的FF算法时间复杂度上界是 O(ef)O(ef) ，其中 ee 为边数，ff 为最大流：

int n, m, s, t; // s是源点，t是汇点 bool vis[MAXN]; int dfs(int p = s, int flow = INF) { if (p == t) return flow; // 到达终点，返回这条增广路的流量 vis[p] = true; for (int eg = head[p]; eg; eg = edges[eg].next) { int to = edges[eg].to, vol = edges[eg].w, c; // 返回的条件是残余容量大于0、未访问过该点且接下来可以达到终点（递归地实现） // 传递下去的流量是边的容量与当前流量中的较小值 if (vol > 0 && !vis[to] && (c = dfs(to, min(vol, flow))) != -1) { edges[eg].w -= c; edges[eg ^ 1].w += c; // 这是链式前向星取反向边的一种简易的方法 // 建图时要把cnt置为1，且要保证反向边紧接着正向边建立 return c; } } return -1; // 无法到达终点 } inline int FF() { int ans = 0, c; while ((c = dfs()) != -1) { memset(vis, 0, sizeof(vis)); ans += c; } return ans; }

要注意，网络流算法的效率是玄学……虽然这个算法的复杂度上界非常高，但在随机图上表现也不算不可接受，至少可以通过洛谷模板题。当然，还有很多优化空间。

Edmond-Karp算法

其实，EK算法就是BFS实现的FF算法。明白这一点后就可以直接看代码了：

int n, m, s, t, last[MAXN], flow[MAXN]; inline int bfs() { memset(last, -1, sizeof(last)); queue<int> q; q.push(s); flow[s] = INF; while (!q.empty()) { int p = q.front(); q.pop(); if (p == t) // 到达汇点，结束搜索 break; for (int eg = head[p]; eg; eg = edges[eg].next) { int to = edges[eg].to, vol = edges[eg].w; if (vol > 0 && last[to] == -1) // 如果残余容量大于0且未访问过（所以last保持在-1） { last[to] = eg; flow[to] = min(flow[p], vol); q.push(to); } } } return last[t] != -1; } inline int EK() { int maxflow = 0; while (bfs()) { maxflow += flow[t]; for (int i = t; i != s; i = edges[last[i] ^ 1].to) // 从汇点原路返回更新残余容量 { edges[last[i]].w -= flow[t]; edges[last[i] ^ 1].w += flow[t]; } } return maxflow; }

为什么在这里BFS通常比DFS的效果好？因为DFS很可能会“绕远路”，而BFS可以保证每次找到的都是最短的增广路。它的复杂度上限是 O(ve2)O(ve^2) ，其中 vv 为点数。这个算法至少与流的大小无关了，算是多项式算法了，让人稍微安心了一点……

Dinic算法

然而，最常用的网络流算法是Dinic算法。作为FF/EK算法的优化，它选择了先用BFS分层，再用DFS寻找。它的时间复杂度上界是 O(v2e)O(v^2e) 。所谓分层，其实就是预处理出源点到每个点的距离（注意每次循环都要预处理一次，因为有些边可能容量变为0不能再走）。我们只往层数高的方向增广，可以保证不走回头路也不绕圈子。

我们可以使用多路增广节省很多花在重复路线上的时间：在某点DFS找到一条增广路后，如果还剩下多余的流量未用，继续在该点DFS尝试找到更多增广路。

此外还有当前弧优化。因为在Dinic算法中，一条边增广一次后就不会再次增广了，所以下次增广时不需要再考虑这条边。我们把head数组复制一份，但不断更新增广的起点。

int n, m, s, t, lv[MAXN], cur[MAXN]; // lv是每个点的层数，cur用于当前弧优化标记增广起点 inline bool bfs() // BFS分层 { memset(lv, -1, sizeof(lv)); lv[s] = 0; memcpy(cur, head, sizeof(head)); // 当前弧优化初始化 queue<int> q; q.push(s); while (!q.empty()) { int p = q.front(); q.pop(); for (int eg = head[p]; eg; eg = edges[eg].next) { int to = edges[eg].to, vol = edges[eg].w; if (vol > 0 && lv[to] == -1) lv[to] = lv[p] + 1, q.push(to); } } return lv[t] != -1; // 如果汇点未访问过说明已经无法达到汇点，此时返回false } int dfs(int p = s, int flow = INF) { if (p == t) return flow; int rmn = flow; // 剩余的流量 for (int eg = cur[p]; eg && rmn; eg = edges[eg].next) // 如果已经没有剩余流量则退出 { cur[p] = eg; // 当前弧优化，更新当前弧 int to = edges[eg].to, vol = edges[eg].w; if (vol > 0 && lv[to] == lv[p] + 1) // 往层数高的方向增广 { int c = dfs(to, min(vol, rmn)); // 尽可能多地传递流量 rmn -= c; // 剩余流量减少 edges[eg].w -= c; // 更新残余容量 edges[eg ^ 1].w += c; // 再次提醒，链式前向星的cnt需要初始化为1（或-1）才能这样求反向边 } } return flow - rmn; // 返回传递出去的流量的大小 } inline int dinic() { int ans = 0; while (bfs()) ans += dfs(); return ans; }

值得注意的是，这个算法如果用在二分图中复杂度是 O(ve)O(v\sqrt e) ，优于匈牙利算法。

这里再提一下最大流最小割定理。所谓割，就是从网络中选择一些边，使得去掉这些边后，剩下两个不连通的分别包含源点和汇点的点集。割的大小是这些边的容量之和。在所有可行的割中，最小的割称为最小割。

这个神奇的定理只有短短几个字：最大流等于最小割。利用这个定理可以解决不少网络流的问题，在此不作证明，想看证明可以看这里。

有人会做一个比喻，割就是恐怖分子切断自来水厂到你家之间的水管（你们恐怖分子就这点志向吗？），切断每个水管的代价就是水管的宽度（边的容量）。然后当代价最小时，从切断的水管中流出的流量之和就是最大流。

说起来，我有某种直觉，很多定理，例如König定理、Dilworth定理和现在这个最大流最小割定理，它们之间隐约仿佛有种共同点。或许它们背后有什么共同的数学背景……？当然也可能是我过度联想（划掉

这篇文章只介绍了网络流的基础内容，其实光是求最大流就有很多优化算法这里没有提到。而且，网络流最难的地方其实在于建模，有很多看似毫不相关的题目都可以建立网络流的模型。如果想见识一下，刷一刷网络流24题吧。这篇笔记就先写到这里。

Pecco：算法学习笔记（目录）2879 赞同 · 94 评论文章

本文地址：https://idcdaohang.com/cloudnews/33077.html

发表评论：

评论记录：

未查询到任何数据！