针对Transformer，谷歌DeepMind一项新的发现引起了不小争议：

它的泛化能力，无法扩展到训练数据以外的内容。

目前这一结论还没有进一步得到验证，但已经惊动了一众大佬，比如Keras之父Francois Chollet表示，如果消息为真，将成为大模型界的一件大事。

谷歌Transformer是今天大模型背后的基础架构，我们所熟悉的GPT里的“T”指的就是它。

一系列大模型表现出强大的上下文学习能力，可以快速学习示例并完成新的任务。

但现在，同样来自Google的研究人员似乎指出了它的致命缺陷——超出训练数据也就是人类已有知识之外，全都无能为力。

一时间，不少从业者认为AGI再次变得遥不可及。

然而，也有网友找出论文中更多关键却被忽略的细节，比如只做了GPT-2规模的试验，训练数据也不是语言等。

随着时间的推移，更多认真研究了这篇论文的网友则指出，研究结论本身没什么问题，但人们却基于此做出过度的解读。

而论文引发网友热议之后，其中一名作者也出来做了两点澄清：

此后，又有网友在Colab中重复了这一实验，却得到了完全不同的结果。

那么，我们就先来看看这篇论文，还有提出不同结果的Samuel，到底都说了什么。

新函数几乎无法预测

实验中，作者在基于Jax的机器学习框架上训练了规模接近GPT-2、只包含解码器的Transformer。

其中包括了12层，8个注意力头，嵌入空间维度为256，参数量约为950万。

为了测试它的泛化能力，作者使用了函数作为测试对象——将线性函数和正弦函数一起作为训练数据喂模型。

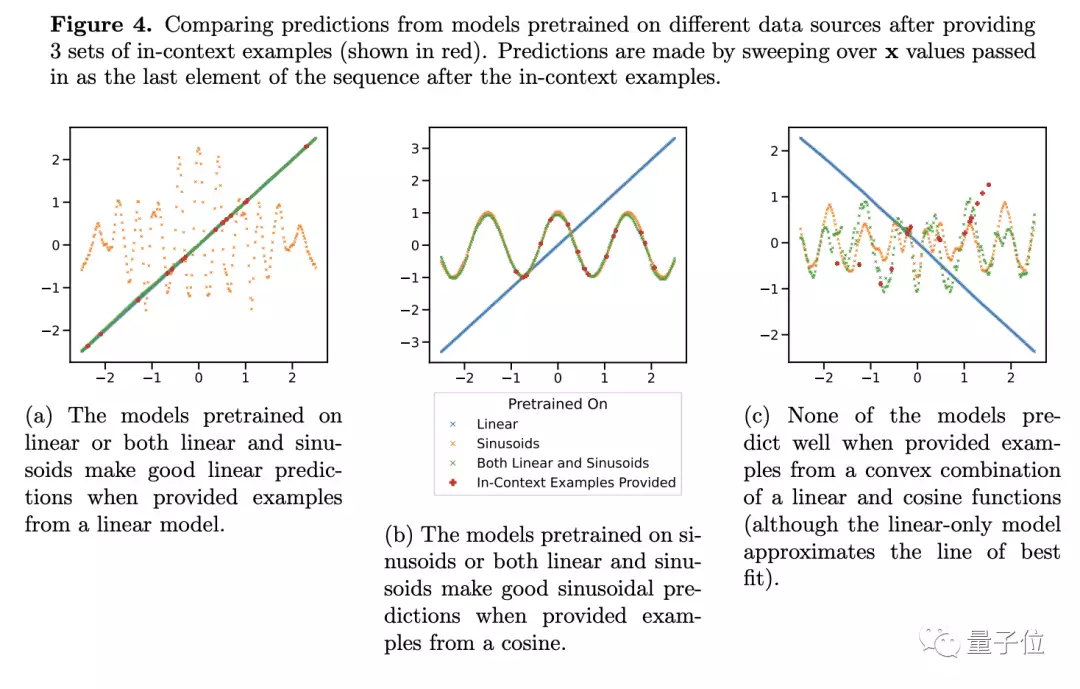
这两种函数对于此时的模型来说是已知，预测的结果自然也很好，但当研究者把线性函数和正弦函数进行了凸性组合时，问题就出现了。

凸性组合并没有那么神秘，作者构建出了形如f(x)=a·kx+(1-a)sin(x)的函数，在我们看来不过是两个函数按比例简单相加。

但我们之所以会这么认为，正是因为我们的大脑拥有这方面的泛化能力，而大模型就不一样了。

别看就是简单相加，对于只见过线性和正弦函数的模型来说，这就是一种全新的函数。

对于这种新函数，Transformer给出的预测可以说是毫无准确性可言（图4c）——于是作者就认为模型在函数上没有泛化能力。

为了进一步验证自己的结论，作者调整了线性或正弦函数的权重，但即使这样Transformer的预测表现也没有显著的变化。

只有一点例外——当其中一项的权重接近1时，模型的预测结果和实际就比较吻合了。

但权重为1意味着，陌生的新函数直接变成了训练时见过的函数，这样的数据对于泛化能力来说显然没有什么意义。

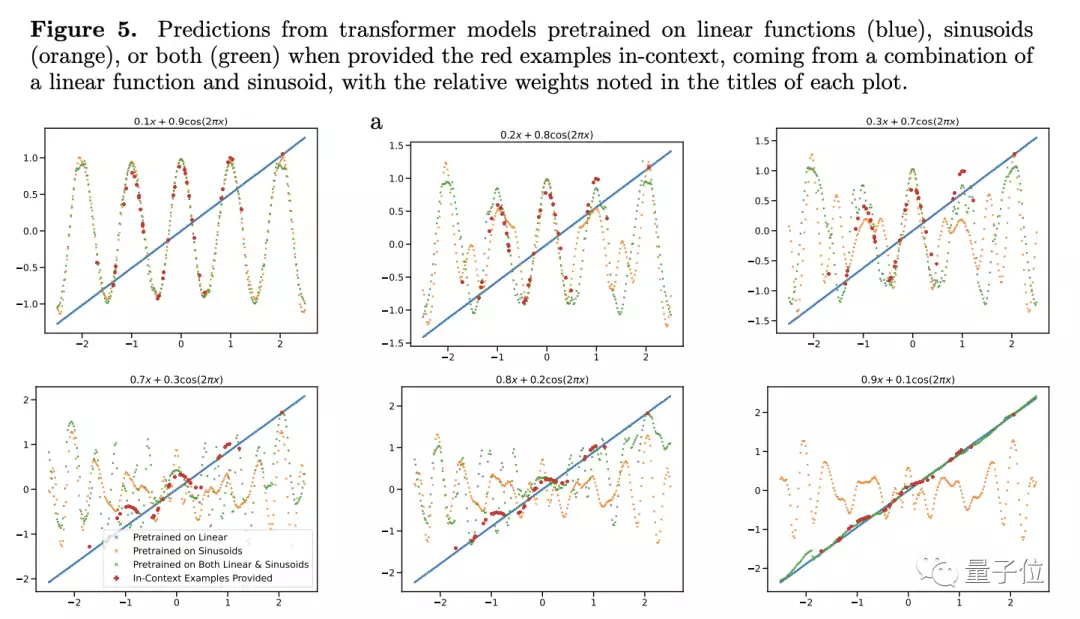
进一步实验还显示，Transformer不仅对于函数的种类十分敏感，甚至同种函数也可能变成陌生条件。

研究人员发现，哪怕是单纯的正弦函数，只是改变其中的频率，模型的预测结果也会发生线束变化。

只有当频率接近训练数据中的函数时，模型才能给出比较准确的预测，当频率过高或过低时，预测结果出现了严重的偏差……

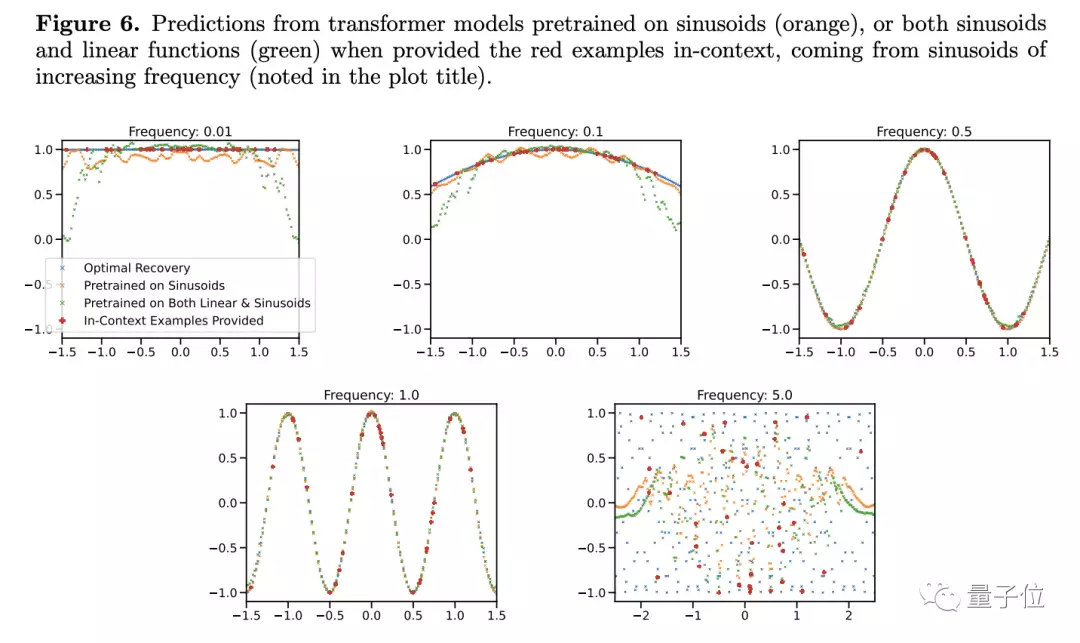
据此，作者认为，条件只要稍微有点不一样，大模型就不知道怎么做了，这不就是说明泛化能力差吗？

作者在文中也自述了研究中存在的一些局限性，如何将函数数据上的观察应用到token化的自然语言问题上。

团队也在语言模型上尝试了相似的试验但遇到一些障碍，如何适当定义任务族（相当于这里的函数种类）、凸组合等还有待解决。

而Samuel这边的模型规模更小，仅有4层，在Colab上训练5分钟后就可以泛化到线性与正弦函数的组合。

不能泛化又如何

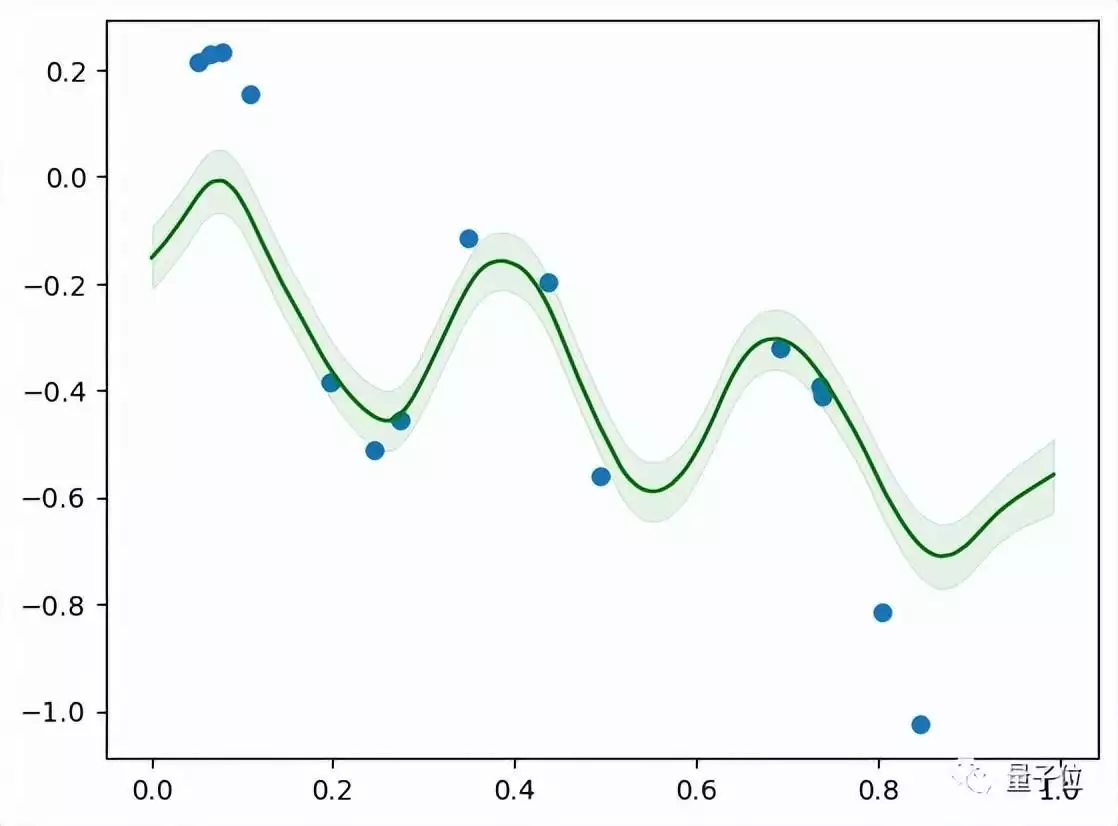
综合全文来看，Quora CEO这篇文章的结论非常窄，只在很多假设下才能成立。

斯隆奖得主、UCLA教授顾全全说，这篇论文本身的结论不存在争议，但不应该被过度解读。

结合先前的研究，Transformer只是无法泛化到与预训练数据“明显不同”的内容，而实际上，大模型的泛化能力通常用任务多样性和任务复杂性来衡量。

如果仔细追究Transformer的泛化能力，恐怕要让子弹再飞一会儿了。

但是，就算真的缺乏泛化能力，又能怎么样呢？

英伟达AI科学家Jim Fan就说，这种现象其实没啥奇怪的，因为Transformer本来就不是万金油，大模型表现得好，是因为训练数据刚好是我们关心的内容。

Jim进一步补充道，这就好像是在说，用一千亿张猫狗的照片训练视觉模型，接着让模型去识别飞机，然后发现，哇，居然真的不认识诶。

不只是大模型，人类在遇到一些未知任务时也不一定能有解决方案，这是否也说明人类缺乏泛化能力呢？

所以，在目标导向之下，无论是大模型还是人类，最终的目的还是要回到解决问题上来，而泛化只是一种手段。

借用这个表情包的说法，既然泛化能力欠缺，那就把它训练到没有训练之外的数据为止。

那么，对于这项研究，你有什么看法呢？

论文地址：

https://arxiv.org/abs/2311.00871

— 完 —

量子位 QbitAI · 头条号签

相关标签：